Filtrage
numérique
Instruction
Utilisation
Exemple
Principe
Le but de cette page n'est pas de
faire un cours sur le filtrage numérique mais de montrer
comment en faire dans le système FORTH décri
dans
ce site.
Le filtrage numérique est une
des applications principales d'un noyau temps réel. Pour
optimiser les temps de calcul, rien de tel que de travailler avec
des nombres entiers plutôt que des nombres flottants surtou
lorsque l'on veut utiliser un processeur au prix raisonnable.
Ceci conduit à utiliser une cellule de filtrage de type
"biquad" ayant la possibilité de réaliser
tous les filtres d'ordre 2 et pouvant être mise en cascade
avec d'autres cellules pour des filtres d'ordre supérieur:
pour une
cellule biquad, on
a
H(z)
= (a0 + a1*z^-1 +
a2*z^-2)/(1 + b1*z^-1 + b2*z^-2)
correspondant à l'algorithme
y(n) = BIQUAD(x(n)) avec les opérations successives
w(n) = x(n) + b1*w(n-1) + b2*w(n-2)
y(n) = a0*w(n) + a1*w(n-1) + a2*w(n-2)
w(n-2) = w(n-1)
w(n-1) = w(n)
pour un
filtre d'ordre supérieur
à 2, on a
H'(z)
= H1(z)*H2(z)*...*Hm(z)
correspondant à l'algorithme
y(n) = (BIQUADm(...(BIQUAD2(BIQUAD1(x(n)))...))
Il faut maintenant définir
les paramètres du filtre biquad en optimisant la
précision
et la vitesse des calculs. Il y a en fait 5 coefficients a0, a1,
a2, b1, b2 et 2 variables w(n-1), w(n-2). Chaque coefficient es
multiplié par un facteur 2^N de telle sorte que la valeur
absolue du plus grand soit la plus proche possible mais
inférieure
à 32768 car ce nombre équivaut à
-32768 en
format 16 bits signé. Pour un N donné, 2^N
correspond
ainsi à la valeur unité. Tous ces
paramètres
sont fournis par l'adresse d'un tableau de 8 nombres entiers de
16 bits:
adr_biquad
-->
N, a2<<N, b2<<N, w(n-2),
a1<<N, b1<<N,
w(n-1), a0<<N
w(n-1) e
w(n-2) sont initialisés
à 0, l'algorithme de calcul est le suivant:
w(n)
= (x(n)<<N +
b1<<N*w(n-1) +
b2<<N*w(n-2))>>N
y(n) = (a0<<N*w(n) + a1<<N*w(n-1) +
a2<<N*w(n-2))>>N
w(n-2) = w(n-1)
w(n-1) = w(n)
Pour déterminer la valeur de
N, il faut chercher le coefficient le plus grand en valeur absolue
puis le multiplier par 2 tant que cette valeur est inferieure
à 16383 ou le diviser par 2 tant qu'elle es
supérieure
à 32767. On ajoute à N, initialisé
à
0, 1 pour chaque multiplication par 2 ou alors -1 pour chaque
division par 2.
Chaque filtre biquad utilisé
dans une application est ainsi défini par une table de
8 nombres entiers signés (6 mots de 16 bits + 2 mots de 32
bits) et une seule instruction
suffit. Un code source FORTH de l'instruction BIQUAD est disponible
dans le fichier biquad.txt.

Instruction
Une seule
instruction
x[n],adr_biquad BIQUAD y[n]
Calcul
de la sortie y[n] du filtre biquad
décrit par adr_biquad et dont la valeur d'entrée
est x[n]:
-
x[n] est l'échantillon d'entrée,
- adr_biquad est l'adresse des
paramètres du filtre,
adr_biquad --> N a2<<N
b2<<N w[n-2] a1<<N
b1<<N w[n-1] a0<<N
- y[n] est l'échantillon de sortie
calculé comme
suit,
w[n] = [x[n]<<N +
b1<<N*w[n-1] +
b2<<N*w[n-2]]>>N
y[n] = [a0<<N*w[n] +
a1<<N*w[n-1] +
a2<<N*w[n-2]]>>N
w[n-2] = w[n-1]
w[n-1] = w[n]

Utilisation
On peut partir de la fonction de transfer
d'un filtre passe bas du second ordre de Butterworth par exemple:
H(p)
= 1/(p^2 +
1,414*p + 1)
selon la transformation bi-linéaire
p
= K*(1 - z^-1)/(1 + z^-1)
et K = 1/(tang(PI*fc/fe))
avec fc pour fréquence de coupure et fe pour
fréquence
d'échantillonage, on obtient
H(z)
= (1 + 2*z^-1 + z^-2)/((K^2
+ 1,414*K + 1)+(2*(1 - K^2)*z^-1 + (K^2 - 1,414*K + 1)*z^-2)
puis l'algorithme
w(n)
= x(n) - [(2*(1 -
K^2)*w(n-1) + (K^2 - 1,414*K + 1)*w(n-2))/(K^2 + 1,414*K + 1)]
y(n) = (w(n) + 2*w(n-1) + w(n-2))/(K^2 + 1,414*K + 1)
w(n-2) = w(n-1)
w(n-1) = w(n)
Si fc = 50 Hz et fe = 1 KHz, alors
K = 6,314 soit:
w(n)
= x(n) + 1,561*w(n-1)
- 0,639*w(n-2)
y(n) = 0,02*w(n) + 0,04*w(n-1) + 0,02*w(n-2)
Ceci conduit à la table suivante:
14, 329, -10508, 0, 658, 25576, 0, 329.
La table est créée par
la séquence FORTH suivante:
DECIMAL HERE
14 ,
329 , -10508 , 0 2,
658 , 25576 , 0 2,
329 ,
CONSTANT FILTRE_PASSE_BAS_2
w(n-2) et w(n-1) son
mémorisés en mots de 32 bits pour optimiser la
précision des calculs.
Pour calculer la valeur d'un échantillon:
FILTRE_PASSE_BAS_2 BIQUAD
Avec fe = 1 KHz, cette action doi
être réalisée toute les millisecondes.

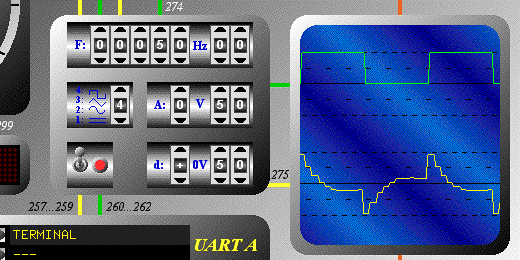
Exemple
Pour illustrer cette page, j'ai
réalisé
le programme biquad.txt et utilisé
la fenêtre système de l'émulateur
du coeur FORTH
et l'application d'affichage de courbes.
Il s'agit de 5 filtres dont la fréquence
de coupure est de 50 Hz et celle d'échantillonage de 1
KHz. Les détails des calculs sont disponibles dans le
fichier
source du programme.
Passe bas du premier ordre:


Passe haut du premier ordre:


Passe bande avec coefficient de
qualité
de 1:


Coupe bande avec coefficient de
qualité
de 1:


Passe bas du deuxième ordre:


Passe haut du deuxième ordre: