Technical
pages
Numerical filtering
Instruction
Use
Example
Principle
The goal of this
page is not to make a lesson on the numerical
filtering but to show how to do it in the FORTH system described
in this web site.
Numerical
filtering is one of the main applications of a
real time kernel. To optimize the computing times, anything of
such as to work with integers rather than floating numbers especially
when we want to use a processor in the moderate price. This implies
to use a filtering cell "biquad" allowing to realize
all the second order filters and and being able to be put in cascade
with other cells for higher order filters:
for a
biquad cell, we have
H(z)
= (a0 + a1*z^-1 +
a2*z^-2)/(1 + b1*z^-1 + b2*z^-2)
corresponding to the algorithm
y(n) = BIQUAD(x(n)) with the successive operations
w(n) = x(n) + b1*w(n-1) + b2*w(n-2)
y(n) = a0*w(n) + a1*w(n-1) + a2*w(n-2)
w(n-2) = w(n-1)
w(n-1) = w(n)
for a more
than order 2 filter,
we have
H'(z)
= H1(z)*H2(z)*...*Hm(z)
corresponding to the algorithm
y(n) = (BIQUADm(...(BIQUAD2(BIQUAD1(x(n)))...))
It is necessary
to define now the biquad filter parameters
with optimization of the computing precision and time. There are
in fact 5 coefficients a0, a1, a2, b1 ,b2 and 2 variables w(n-1),
w(n-2). Each coefficient is multiplied by a 2^N factor in order
to the biggest absolute value is the most possible closed bu
less than 32768 because this number is equal to -32768 in the
16 bits signed format. For a gived N, 2^N is corresponding to
the value unity. All those parameters are furnished through the
address of a 8 16 bits integers table:
adr_biquad
-->
N, a2<<N, b2<<N, w(n-2),
a1<<N, b1<<N,
w(n-1), a0<<N
w(n-1) e
w(n-2) are initialized
to 0, the computing algorithm is the following:
w(n)
= (x(n)<<N +
b1<<N*w(n-1) +
b2<<N*w(n-2))>>N
y(n) = (a0<<N*w(n) + a1<<N*w(n-1) +
a2<<N*w(n-2))>>N
w(n-2) = w(n-1)
w(n-1) = w(n)
To determine
the value of N, we have to search the coefficien
with the great absolute value then multiply it by 2 while this
value is less than 16383 or divide it by 2 while this value is
more than 32767. We add to N, initialized to 0, 1 for each
multiplication
by 2 or -1 for each division by 2.
Each biquad
filter used in an application is so defined
by 8 integers table (6 16 bits words + 2 32 bits words) and only one
instruction is necessary. A FORTH
source code of BIQUAD instruction is
avalaible in the file biquad.txt.

Instruction
Only one
instruction
x[n],adr_biquad BIQUAD y[n]
Computing
of the output y[n] of the biquad
filter described by adr_biquad and with the input value x[n]:
- x[n] is the input sample,
- adr_biquad is the address of the filter
parameters,
adr_biquad --> N a2<<N
b2<<N w[n-2] a1<<N
b1<<N w[n-1] a0<<N
- y[n] is the output sample computed as following,
w[n] = [x[n]<<N +
b1<<N*w[n-1] +
b2<<N*w[n-2]]>>N
y[n] = [a0<<N*w[n] +
a1<<N*w[n-1] +
a2<<N*w[n-2]]>>N
w[n-2] = w[n-1]
w[n-1] = w[n]

Use
We can start from the transfert function
of a Butterworth second order low pass filter for example:
H(p)
= 1/(p^2 +
1,414*p + 1)
following the bi-linear transformation
p
= K*(1 - z^-1)/(1 + z^-1)
et K = 1/(tang(PI*fc/fe))
with the cutting frequency fc and the sampling frequency fe, we
obtains
H(z)
= (1 + 2*z^-1 + z^-2)/((K^2
+ 1,414*K + 1)+(2*(1 - K^2)*z^-1 + (K^2 - 1,414*K + 1)*z^-2)
then the algorithm
w(n)
= x(n) - [(2*(1 -
K^2)*w(n-1) + (K^2 - 1,414*K + 1)*w(n-2))/(K^2 + 1,414*K + 1)]
y(n) = (w(n) + 2*w(n-1) + w(n-2))/(K^2 + 1,414*K + 1)
w(n-2) = w(n-1)
w(n-1) = w(n)
If fc = 50 Hz and fe = 1 KHz, then
K = 6,314 so:
w(n)
= x(n) + 1,561*w(n-1)
- 0,639*w(n-2)
y(n) = 0,02*w(n) + 0,04*w(n-1) + 0,02*w(n-2)
this is corresponding to the following
table: 14, 329, -10508, 0, 658, 25576, 0, 329.
The table is created with the following
FORTH sequence:
DECIMAL HERE
14 ,
329 , -10508 , 0 2,
658 , 25576 , 0 2,
329 ,
CONSTANT FILTRE_PASSE_BAS_2
w(n-2) et w(n-1) are stored with 32 bits
words in order to optimize the computing precision.
To compute
a sample value:
FILTRE_PASSE_BAS_2 BIQUAD
With fe = 1 KHz, this action mus
be realized each milliseconde.

Example
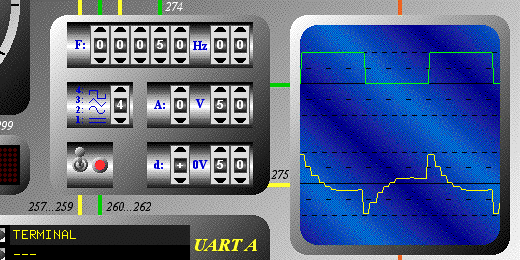
To illustrate this page, I have realized
the software biquad.txt and used
the system window of the FORTH core
emulator. and the curves displaying application.
There are 5 filters with a cutting frequency of 50 Hz and a sampling
frequency of 1 KHz. The detailed calculates are avalaibles in
the software source file.
First order low pass:


First order high pass:


Band pass with quality coefficien
of 1:


Band stop with quality coefficien
of 1:


Second order low pass:


Second order high pass: