Working in the National Look-out post of Radio astronomy of the United States at the beginning of the 70s, Charles Moore was charged to schedule the first minicomputers 16 bits (typify IBM 360) for the purchase of scientific data and the maintenance of equipment.

The high-level languages of time as the FORTRAN (not to confuse with the object of this paragraph) was too heavy for the execution of real-time software packages. Machine language was, as for him, indigestible enough to venture to realize always more complex programs.

And so Charles MOORE had the idea to create a revolutionary language the instructions of bases of which corresponded to a single line of code in machine language.

This allowed not only to write programs in high-level language with almost the performances of machine language but besides reducing at most size memory which was extremely weak at the time.

Charles MOORE wanted to record his language under the name of FOURTH for language of fourth generation but the computer which he used authorizing only names of 5 letters, he called it: FORTH.

Well to understand and to use at most performances inferred by the language FORTH, it is important to master inverted Polish notation used also with calculators made by Hewlett-Packard. The transmission of parameters makes essentially by a last in-firs out stack. This notion is what allowed Charles Moore to pull the maximum of performances of its language because it is necessary to know that any processor deserving of this name possesses memory manipulation instructions under shape of stack of this type.

Besides the classic stack of return from subroutines administered intrinsically with most of the processors, the idea to use the same instructions for parameters transfers drove to create a data stack of which some basic instructions are the following ones:

• DUP piles the copy of the number being at the top of the stack: n - > n, n (the summit of the stack is to the right),
• DROP depilates the number being at the top of the stack: n - > - (line means that the stack is empty with regard to the previous level),
• SWAP inverts the 2 numbers of the summit of the stack: n1 , n2 - > n2 , n1
• OVER piles the copy of the number situated in the second rank of the summit of the stack: n1 , n2 - > n1 , n2 , n1
• ...

Operations such as comparisons or additions will directly consume the numbers situated at the top of the stack:

• > Compare the 2 numbers at the top of the stack and leave a boolean: n1 , n2 - >-1 if n1 > n2 , 0 otherwise
• -Complete subtraction such as: n1 , n2 - > n1-n2
• * Signed complete reproduction such as: n1 , n2 - > n1*n2
• ...

The most control basic structure is the set formed with IF, ELSE AND THEN. IF tests the number at the top of the stack by pulling it. If it is different from 0, instructions placed between IF and ELSE are executed then program connects following the word THEN. If it is zero, program connects directly in instructions being following the word ELSE. Several structures of this type can be obviously been linked.

In FORTH, all the instructions can be programs and mutually. They are introduced into the memory according to their compilation. Put in by some instructions which manipulate the return stack as the structures of control for example, all the instructions can be interpreted at any time what gives considerable opportunities of settling for developers. Useless to write another main program and to redo a compilation to see if it is subroutine which works badly . It is enough to launch his execution with adequate parameters.

Instructions or programs or subroutines are inserted into the memory with pointers' system which connect them among them to allow the interpreter (or in the compiler according to the mode of functioning) to find them. Search begins by leaving of the last compiled instruction and by raising until the first which is often DUP. If instruction does not exist, the interpreter / compiler looks if it is a number and piles it at the top of the stack in interpretation mode or compiles it in the instruction in compilation mode. To create an instruction, one uses 2 instructions (except those that describe the sequence to be executed):

• : Follow-up of the name of the instruction and which spends from interpretation to compilation mode,
• ; Which ends instruction and so goes back in interpretation mode.

Finally, not to be too exhaustive in this presentation, know that FORTH language allows to write recurse procedures what makes a really very evolved language of it. Here is the example of factorial calculation program of an integer appealing to this notion of recursion:

: FACTORIELLE
 DUP 1 >
  IF
   DUP 1 - FACTORIELLE *
 THEN
;

 To illustrate this introduction in the language FORTH, here is a screen presenting the development of this instruction:

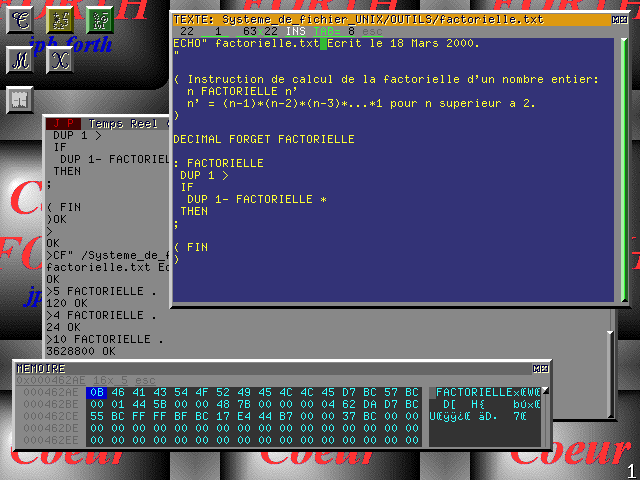
The window of interpretation (in light gray) gives values calculated by the factorials of 5, 4 and 10 after compilation of the file contained in the window of edition (in blue). The window of display of the memory (in dark gray) shows size occupied by this instruction which is of 46 bytes.

To have more information on FORTH, I invite you to consul the Page of links making reference to the main sites of the net.