Transformée
de Fourier rapide
Instructions
Utilisation
Exemple
Principe
La
transformée de Fourier rapide est un outil très
utilisé dans le domaine du traitement de signal. Pour qu'elle
soit relativement rapide, il faut qu'elle soit adaptée au type
de processeur qui doit l'effectuer. J'en ai donc fait une version
optimisée pour les calculs en nombres entiers et utilisant les
fonctions trigonometriques SIN et COS présentées dans la page correspondante.
Pour présenter les résultats que l'on peut en obtenir, j'ai utilisé l'application d'affichage de courbes qui requiert l'utilisation de nombres en virgule flottante 64 bits juste avant l'affichage.
Voici
par exemple la transformée de Fourier d'un signal
sinusoïdal de 2 KHz échantilloné à 512 KHz
pendant 1 ms:


Instructions
ln(nbp)/ln(2) correspond au logarithme en base
2 du nombre de points (exemple: 10 pour nbp=1024)
@temp est l'adresse de la table des nombres complexes dans le domaine
temporel
@freq est l'adresse de la table des nombres complexes dans le domaine
fréquenciel
@temp,ln(nbp)/ln(2) TFR @freq
Transformée
de Foutrier rapide (domaie temporel à
fréquenciel).
@freq est nul si problème (pas assez de mémoire
disponible ou bien ln(nbp)/ln(2) inférieur ou
égal
à zéro)
@freq,ln(nbp)/ln(2) TFR-1 @temp
Transformée
de Foutrier rapide inverse (domaine fréquenciel à
temporel).
@freq est nul si problème (pas assez de mémoire
disponible ou bien ln(nbp)/ln(2) inférieur ou
égal
à zéro)

Utilisation
Ces
fonctions sont optimisées pour manipuler des nombres entiers de
16 bits avec des calculs internes sur 32 bits pour limiter la
propagation des erreurs d'arrondi. Les paramètres
d'entrée sont un pointeur (@temp ou @freq) sur une table de
nombres entiers entiers 16 bits complexes (a+bi) et la taille n
(ou ln(nbp)/ln(2)) qui est une puissance de 2:
| @temp ou @freq |
--> |
a(1),b(1) |
| @temp ou @freq +4 |
--> |
a(2),b(2) |
| @temp ou @freq +8 |
--> |
a(3),b(3) |
| ... |
... |
... |
| @temp ou @freq +4*(2^n-1) |
--> |
a(2^n),b(2^n) |
Dans le
domaine temporel (@temp), il suffit d'initialiser les a(n) par les
échantillons du signal en mettant tous les b(n) à 0. Les
fonctions TFR et TFR-1 allouent de la mémoire (avec
l'instruction MEMOIRE_ALLOUE) qu'il ne faudra pas oublier de
libérer (MEMOIRE_LIBERE) dès que le résultat ne
sera plus utilisé.
Déterminons
par exemple la transformée de Fourier d'un signal
sinusoïdal de 2 KHz sur 512 points, il faut commencer par
générer la table des 512 échantillons:
2 512 * ALLOT CONSTANT @SINUS ( 1024 mots de 16 bits )
0 VARIABLE @FREQ
0 VARIABLE @TEMP
: SINUS_2KHz_512
512 0 DO
I 32768 256 */ SIN 1000 32768 */ @TEMP I 4* + ! ( calcul des a(n) avec une amplitude de 1000 )
0 @SINUS I 4* + 2+ ! ( calcul des b(n) )
LOOP
;
SINUS_2KHz_512
Il n'y a plus qu'à lancer la transformée de Fourier:
@SINUS 9 TFR ( fournit l'adresse de la table des résultats dans le domaine fréquentiel ) @FREQ 2!
On peut ensuite retrouver le signal d'origine en lançant la transformée de Fourier inverse:
@FREQ 2@ 9 TFR-1 ( fournit l'adresse de la table des résultats dans le domaine temporel ) @SINUS 2!
Dès que les résultats sont exploités, il ne faut pas oublier de libérer la mémoire:
@FREQ 2@ MEMOIRE_LIBERE DROP @TEMP 2@ MEMOIRE_LIBERE
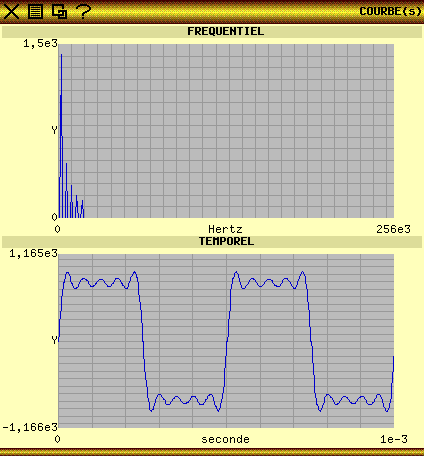
La
capture d'écran suivante donne la représentation
graphique d'une transformée de Fourier inverse de 512 points
reconstituant un signal rectangulaire à partir de la
fréquence fondamentale et les 4 premières harmoniques
(impaires):
Cette capture d'écran
donne celle reconstituant un signal triangulaire à partir de la
fréquence fondamentale et des 4 premières harmoniques:


Exemple
Voici
par exemple une étude de plusieurs types de modulations
utilisant le programme fichier fft.txt. Les courbes
présentées dans cette page sont de 1024 points, le
programme permet de les calculer aussi en 256, 512, 2048 et 4096 points.
Tout d'abord, le signal modulant f(t) qui est la somme de 5 sinusoïdales de 3, 6, 9, 12 et 15 KHz:

Voici maintenant la porteuse F(t), une sinusoïdale de 80 KHz:

La modulation d'amplitude (MA):


La modulation d'amplitude à porteuse supprimée (MAPS):


Et enfin la modulation d'amplitude à bande latéral unique (BLU):



